Summary
The Taxicab Problem, presented by Amos Tversky and Daniel Kahneman in 1982, is a classic example in probability theory that illustrates base rate neglect, a cognitive bias where people overlook the actual statistical base rate in favor of specific information.
What does it mean for everyday problem-solving?
The probability of an event occurring must take into account all known variables. There is no such thing as an independent event with an absolute likeliness.
The Problem
In a city, 85% of the taxis are green and 15% are blue. A witness claims they saw a blue taxi involved in a hit-and-run accident. The witness’s ability to correctly identify the color of a taxi is tested, and they are correct 80% of the time, but they also make mistakes 20% of the time.
Question
What is the probability that the taxi involved was actually blue?
Solution
This is a Bayesian probability problem. The key is to combine the base rate of the taxis (green vs. blue) with the reliability of the witness:
- Base rate (prior probability): 15% for blue taxis.
- Witness reliability: 80% correct for identifying blue taxis.
Using Bayes’ theorem, the correct answer shows that the probability of the taxi actually being blue is about 41%, not 80%, demonstrating how people often misjudge probabilities by focusing on the witness’s accuracy rather than integrating the base rate.
Here’s the step-by-step calculation using Bayes’ theorem:
1. Definitions:
Let’s define:
- B: Event that the taxi is blue.
- G: Event that the taxi is green.
- W: Event that the witness says the taxi is blue.
We need to find the probability that the taxi is actually blue given that the witness said it was blue, .
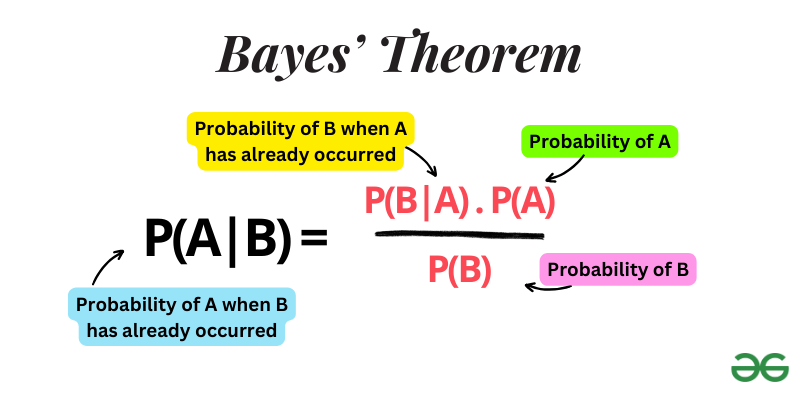
2. Bayes’ Theorem Formula:
 Source: https://www.geeksforgeeks.org/real-life-applications-of-bayes-theorem
Source: https://www.geeksforgeeks.org/real-life-applications-of-bayes-theorem
P(B|W)=[P(W|B)∗P(B)]/P(W)
Where:
- P(B|W) is the probability the taxi is blue given the witness says it’s blue.
- P(W|B) is the probability the witness says the taxi is blue when it actually is blue.
- P(B) is the base rate (prior probability) of the taxi being blue.
- P(W) is the total probability of the witness saying the taxi is blue.
3. Known Values:
- P(B) = 0.15 (15% of the taxis are blue)
- P(G) = 0.85 (85% of the taxis are green)
- P (W|B) = 0.8 (80% accuracy when the taxi is actually blue)
- P (W|G)= 0.2 (20% error when the taxi is actually green)
4. Compute P(W)
P(W) = Total Probability of Witness Saying “Blue”
Plugging in the values:
P(W)= P(W|B)xP(B) + P(W|G)xP(G)=0.8x0.15 + 0.2x0.85=0.29
5. Apply Bayes’ Theorem
P(B|W)=(0.8x0.15)/0.29=~0.414
Result
The probability that the taxi is actually blue, given the witness said it was blue, is approximately 41.4%.
You might also wanna check out a cool simulation of this problem